쿠팡파트너스 활동으로 수수료를 제공받을 수 있습니다.
LSMC(Least Square Monte Carlo)
Monte Carlo + Least Square
조기상환 옵션을 가진 Note의 이론가 계산에 사용하는 방법
LSMC, Longstaff Schwartz Method
ChatGPT로 쉽게 배우는 LSMC 아메리칸 풋옵션 프라이싱
import numpy as np
from scipy.stats import norm
import numpy.polynomial.polynomial as poly
def simulate_asset_paths(S0, r, sigma, T, M, I):
"""
Simulate I asset paths with M time steps over the time horizon T.
"""
dt = T / M
paths = np.zeros((M + 1, I))
paths[0] = S0
for t in range(1, M + 1):
z = np.random.standard_normal(I)
paths[t] = paths[t - 1] * np.exp((r - 0.5 * sigma ** 2) * dt + sigma * np.sqrt(dt) * z)
return paths
def LSM_american_option(S0, K, T, r, sigma, M, I):
"""
Least Squares Monte Carlo simulation for American option pricing.
"""
dt = T / M
discount = np.exp(-r * dt)
paths = simulate_asset_paths(S0, r, sigma, T, M, I)
# Payoff at maturity (option intrinsic value)
payoff = np.maximum(K - paths, 0)
# Initialize the option value matrix
V = np.zeros_like(payoff)
V[-1] = payoff[-1]
# Backward induction
for t in range(M - 1, 0, -1):
reg = np.polyfit(paths[t], V[t + 1] * discount, 2) # Least squares regression
continuation_value = np.polyval(reg, paths[t]) # Calculate the continuation value
V[t] = np.where(payoff[t] > continuation_value, payoff[t], V[t + 1] * discount) # Optimal stopping decision
# Estimating the option price
option_price = np.mean(V[1] * discount)
return option_price
# Parameters
S0 = 100 # Initial stock price
K = 100 # Strike price
T = 1 # Time to maturity in years
r = 0.05 # Risk-free rate
sigma = 0.2 # Volatility
M = 50 # Number of time steps
I = 10000 # Number of paths
option_price = LSM_american_option(S0, K, T, r, sigma, M, I)
print(f"American Option Price: {option_price}")
Python
복사
코드의 로직
1.
시점 에 대하여, 개의 GBM path를 생성한다.
2.
옵션 만기 시점 에서의 option value는 행사가치인 payoff로 놓는다.
3.
부터 까지 Backward Induction으로 각각의 시점 마다 각 path의 option value를 결정한다.
4.
에서 구해진 각 path 에서의 option value에 기댓값을 취하고, discount 하면, 에서의 옵션 가격이 구해진다.
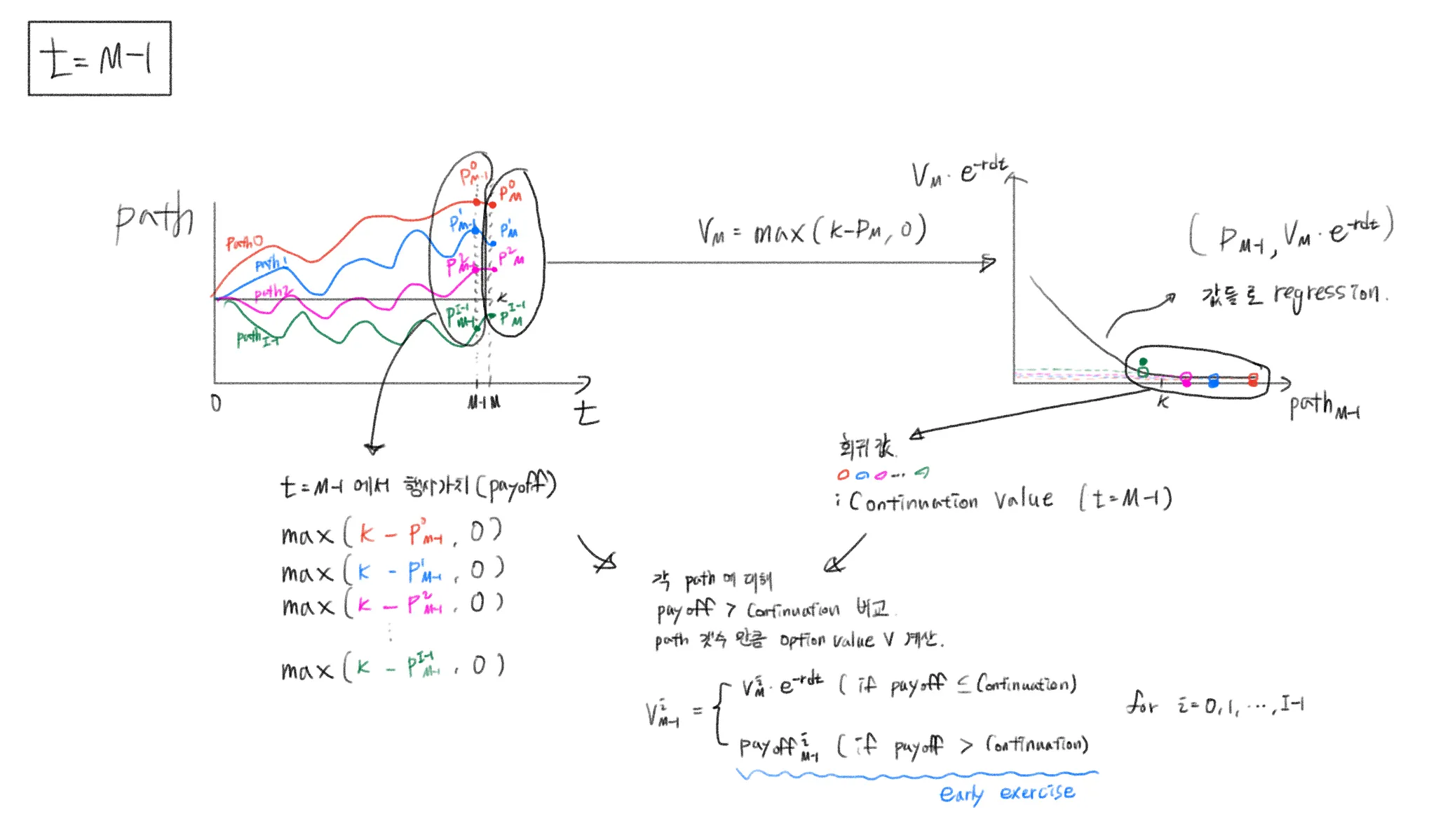
Backward Induction
# Backward induction
for t in range(M - 1, 0, -1):
reg = np.polyfit(paths[t], V[t + 1] * discount, 2) # Least squares regression
continuation_value = np.polyval(reg, paths[t]) # Calculate the continuation value
V[t] = np.where(payoff[t] > continuation_value, payoff[t], V[t + 1] * discount) # Optimal stopping decision
Python
복사
regression을 이용해 개 path에 대하여 continuation을 구하고, 각 path마다 payoff[t] > continuation를 비교하여,
True → V[t] = payoff[t]
False → V[t] = V[t + 1] * exp(-r * dt)